
All these example are real MGS programs. Please refer to the documentation
available at the MGS home page
to access the actual programs and interpreter. A lot of additional examples
are available, e.g. in the MGS tutorial.
The vizualisation of the outputs is done using several post-processing
tools: mathematica, imoview (the MGS 3D scene description
language and viewer), asciitopgm, etc.

|
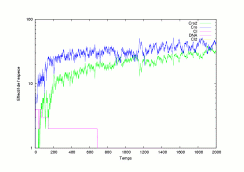
Switch of the phage lambda using Gillespie's SSAStochastic simulation is
of interest when the number of molecules and/or the time-step between
each event of the modelized system is small. The lambda phage is a
virus that infects the cells of the Escherichia coli
bacteria. Once having infected the bacteria, the virus has two possible
developmental pathways. It can either (1) replicate and lyse (dissolve) the host cell an release about 100 progeny or (2) integrate its DNA into the bacterial DNA and form a lysogen.
We describe the modelization and simulation in MGS of this phenomenon
using a stochastic rule application strategy following Gillespie's Stochastic Simulation Algorithm.
|

|
BEAD-sort (animation)Bead sort is a new sorting algorithm designed by
J. J. Arulanandham, C. S. Calude and M. J. Dinneen (EATCS Bull. 76 (2002)).
The idea is to represent positive integers by a set of beads, like those
used in an abacus. Beads are attached to vertical rods and appear to be
suspended in the air just before sliding down (a number is read horizontally,
as a row). After their falls, the rows of numbers have been rearranged such
as the smaller numbers appears on top of greater numbers.
|

|
Snowflake formation (animation)A simplified cellular automata on an hexagonal grid that mimics the growth of a snowflake. |
|
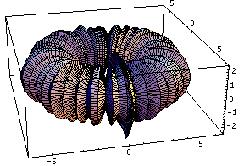
Diffusion-reaction a la Turing in a ring of cells (animation)This bubling torus is a visual representation of a diffusion-reaction process "à la Turing" on a ring of cells. A very simple MGS program is used to compute the density of two chemicals that diffuse and react on a ring of cells. The data are then written in a file together with a simple Mathematica program used to generate this plot. The diameter of the torus is proportional to the density of one of the chemicals. A bigger animated version (3Mb animated gif) is available. |

|
Diffusion-reaction a la Turing at the surface of a torus (animation)
Same model as the previous one, but the diffusion occurs at the
surface of a torus. In the graphical representation, the height of a point
at the surface of the torus is proportional to the density of one of the
chemicals. A bigger animated version (3Mb animated
gif) is available.
|

|
Turing reaction-diffusion driving the cell division in a filament of cells
This picture visualizes a Turing-like
reaction-diffusion process on a line of cells, but one of the two
chemicals is used as a trigger of the cell division. When its level is
above a given threshold, the cell divides into two cells.
|

|
Heterocysts differentiation during Anabaena growth
The cyanobacterium Anabaena grows in filaments of 100
cells or more. When starved for nitrogen, specialized cells called heterocysts
differentiate from the photosynthetic vegetative cells at regular intervals
along each filament. Heterocysts are anaerobic factories for nitrogen
fixation; in them, the nitrogenase enzyme complex is synthesized and the
components of the oxygen-evolving photosystem II are turned off. Plant
signals exert both positive and negative regulatory control on heterocyst
differentiation.
|

|
Modeling of a spatially distributed signaling pathway
The modeling approach of a signaling pathway is proposed
by Bugrim (A Logic-based Approach for Computational Analysis of Spatially
Distributed Biochemical Networks, Andrej Bugrim, ISMB 2000) and takes
into account the spatial localisation of the molecules. The reaction, diffusion
and transport processes described in the Bugrim model are modeled as multiset
transformations taking place in a nest of multisets. This is reminiscent
of the P system approach.
|

|
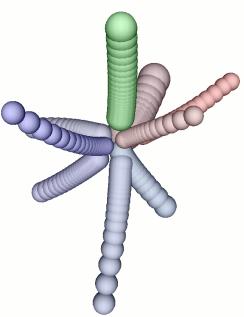
Flocking birds
This model is an attempt to mimic the flocking of birds. (The
resulting motion also resembles schools of fish.) The flocks that appear
in this model are not created or led in any way by special leader birds.
Rather, each bird is following exactly the same set of rules, from which
apparent flocks emerge.
|
|
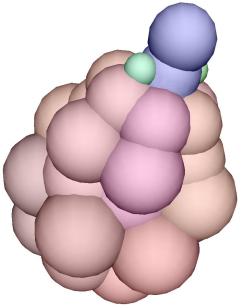
Moving cells linked by a spring force
Each sphere in the picture below corresponds to a cell attracted
by its neighboring cells by a spring. The neighborhood of a cell is computed
dynamically using a Delaunay graph built from the cells position. At each
time step, this neighborhood can change.
|
|
Phenomenological sketch of the growth of a meristeme
The meristem is an undifferentiated plant tissue from which
new cells are formed, as at the tip of a stem or root. Some of these cells,
driven by flux of hormones, divide and differentiate to form all the plant's
organs.
In this rough sketch, two parallel processes take place :
|
|
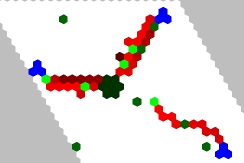
Colonies of ants foraging for food in MGS (animation)In this project, a colony of ants forages for food. The ant behavior follows a set of MGS rules, but the colony as a whole acts in a sophisticated way.
When an ant finds a piece of food, it carries the food back to the
nest, dropping a chemical as it moves. When other ants "sniff" the
chemical, they follow the chemical toward the food. As more ants carry
food to the nest, they reinforce the chemical trail.
(blue = food, green = ant, red = chemical, black = nest.)
This program can be run on a NEWS grid or on an hexagonal pavement of the plane. |

|
Blob computing in MGS (animation)
The BLOB Computing project,
developped by F. Gruau, represents an alternative to the current Von
Neumann model, following a biocomputation dogma. Blobs are
dynamic spatial domain of computation. The short animation shows the
collision of two blobs in the space of computation.
An initial simulator of blobs has been build using a cellular automata. The results presented are based on an MGS simulator using the proxi collection kind. |
|
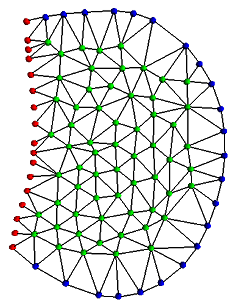
Simulation of Ascaris Suum sperm crawling (animation)In this example, we are interested in impementing a complex biological model inpired from the work of Bottino et al. This model simulates the sperm motility of the nematod Ascaris suum. The Ascaris suum sperm cell crawls using a lamellipodial protusion, adhesion, retraction cycle. Bottino describes this process within continuous differential equations. They correspond to the elastic and tensile stress in the membrane fixed to the extracellular matrix, and to pH distribution to deal with the pH dependence. In a second step, these equations are translated into a discrete form through a finite element model. The membrane is divided with a Delaunay graphe. The translation of this discrete membrane using MGS topological collections and transformations is straightforward. |

|
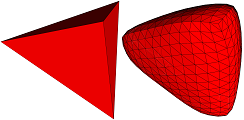
Cellular automata and cellular complexes (animation)Cellular complexes allow to create various kinds of neighborhood. One of the advantages of MGS is applying a transformation dedicated to a homogeneous topological collection (as GBF collections are, where each element has a constant number of neighbors), on a topological collection whose neighborhood is heterogeneous. As an example, we see the application of transformations that correspond to cellular automata, on 3D geometrical meshes. |
|
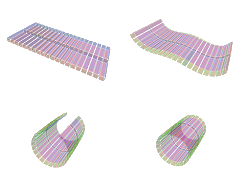
Surface subdivisionIn this example, transformations are used to declaratively and locally describe a subdivision algorithm and keep a good expressiveness. We focus here on one of the simplest algorithms of triangular meshes subdivision, the polyhedral one. It consists in dividing each triangle into four triangles. |
|
Declarative modeling of a neurulation-like process (animation)During pluricellular organism growth, two characteristics are interesting to be highlighted: (1) local and individual behavior generates a global transformation, (2) the global transformation can lead to a topological modification of the structure. In this example, we want to show how MGS can be used to implement these kind of complex phenomena. We will especially focus on the neurulation process. |

Pictures, graphics and animations are licensed under a Creative Commons License.
|
|