Flocking birds in MGS



Principles

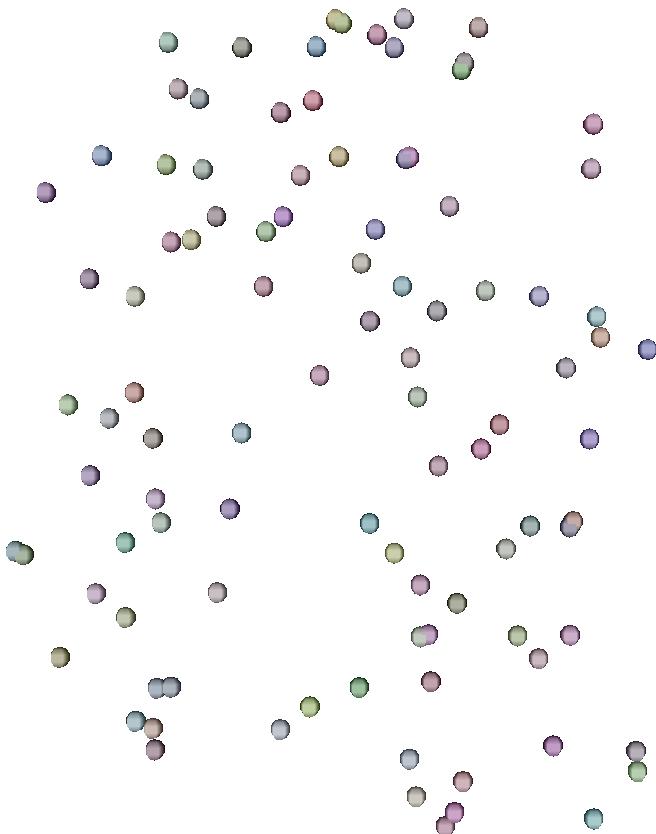
This model is inspired by a simulation of flocking birds proposed by U.Wilensky and by the development of steering behaviors of boids (generic simulated flocking creatures) invented by C. Reynolds. The algorithm we use here is roughly similar to the algorithm they uses, but it is not the same.
The idea is to mimic the flocking of birds. The resulting motion also resembles schools of fish. The flocks that appear in this model are not created or led in any way by special leader birds. Rather, each bird is following exactly the same set of rules, from which apparent flocks emerge. The basic flocking model consists of three simple steering behaviors which describe how an individual boid maneuvers based on the positions and velocities its nearby flockmates:

  1. separation : when a birds is to close of a neighbor, it changes of direction
  2. cohesion : when a birds is to far from one of its neighbor, it try to join quickly the fartest
  3. alignment : when the neighbors of a birds are neither too far or to close, the bird chose a direction which is te average of the direction of its neighbors.

For the sake of the simplicity, the birds moves in a 2D plane. Each bird follows some direction at the same constant speed. This speed is increased when it tries to reach a neighbor to far. The neighbors of a bird in the 2D space are computed using a Delaunay triangulation (you can compute delaunay triangulation on-line thanks to this java-applet). In MGS, the Delaunay collection type is a collection of points (in an euclidean space) whose neighborhood relationships are computed by a delaunay triangulation.This collection type is used to represents the birds.

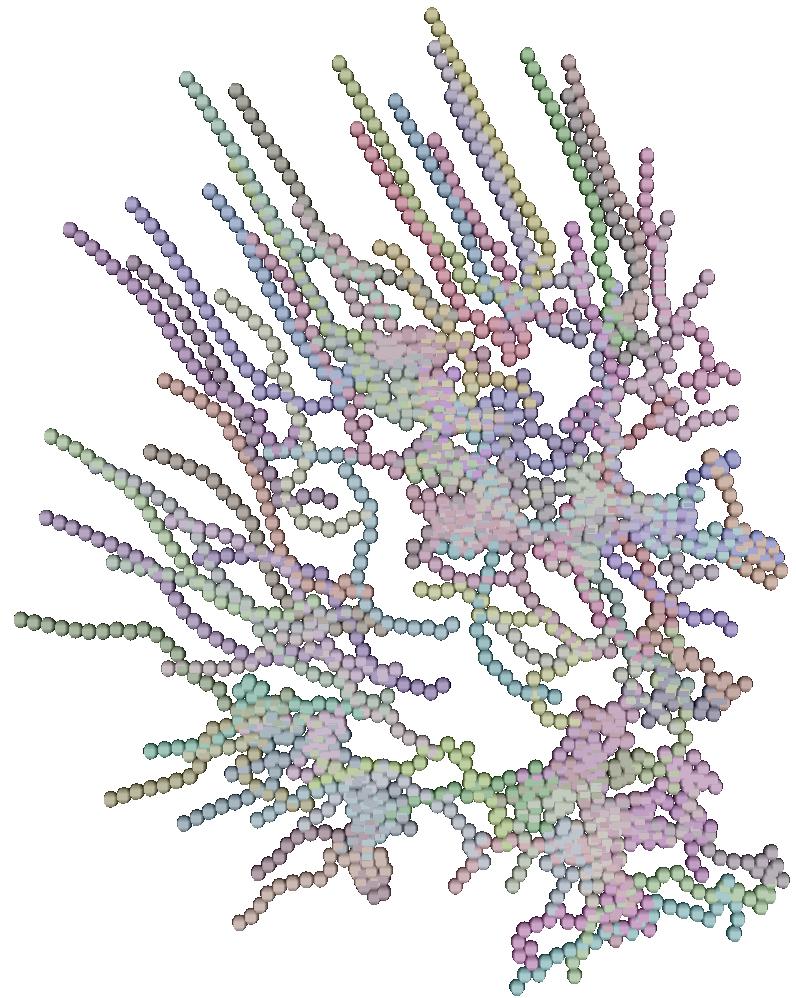
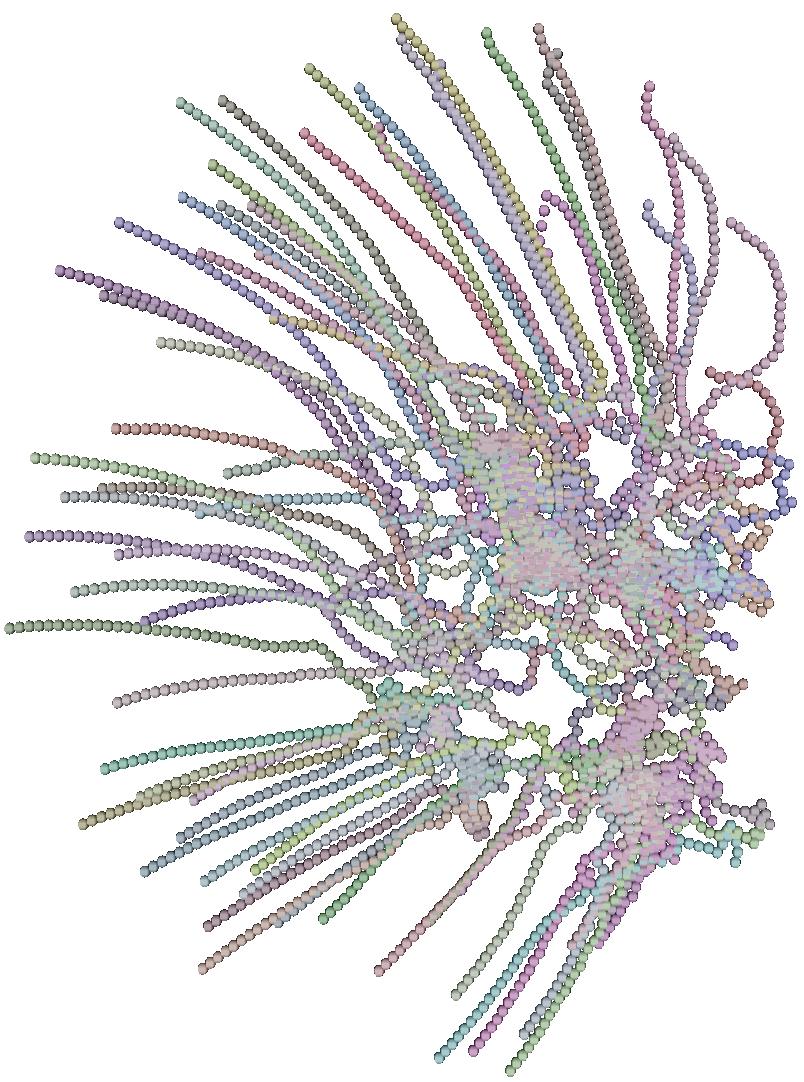
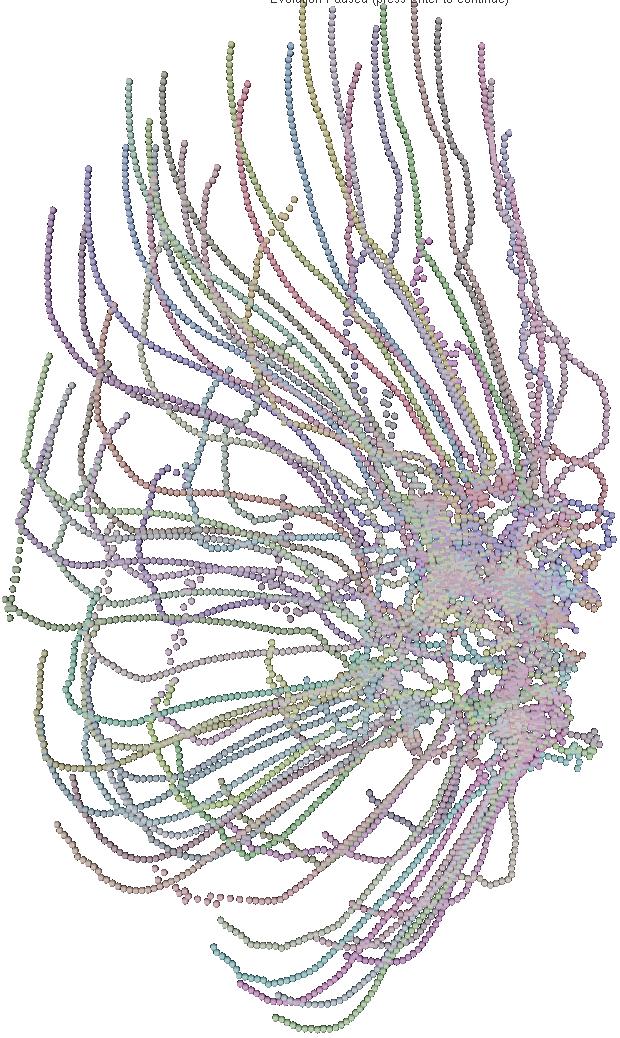
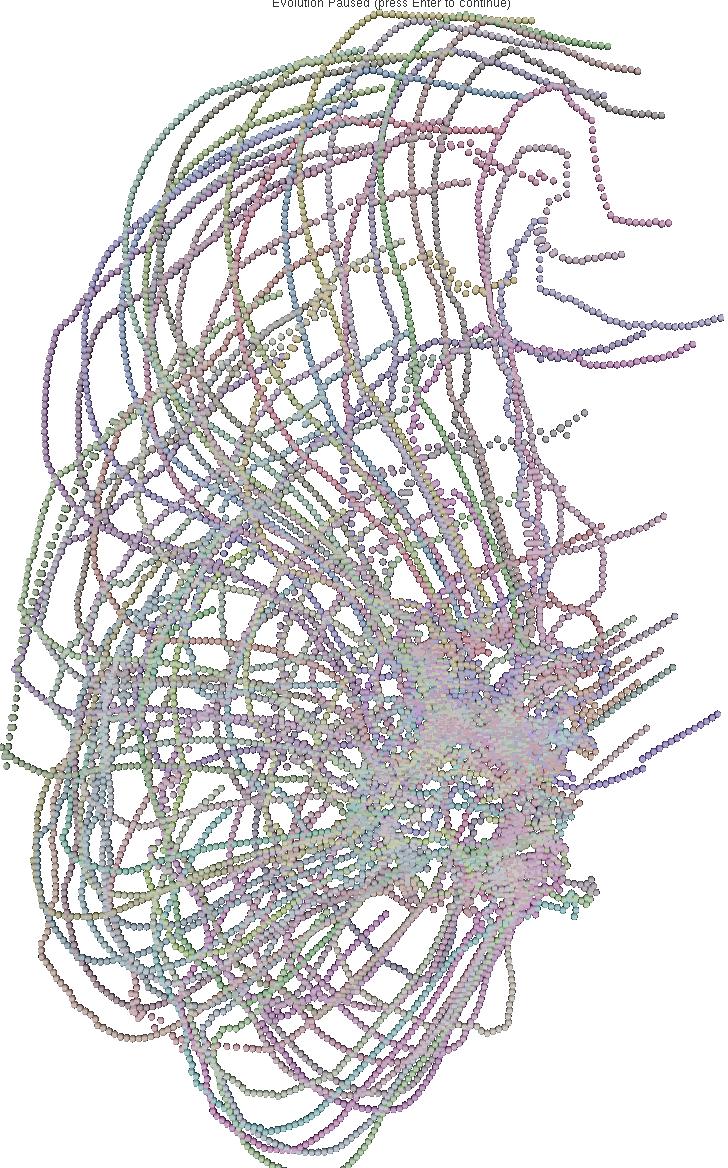
The 6 pictures below are the record of the trajectory followed by 50 birds shoot ate several time step. The position and direction followed by the birds at t=0 (first picture) are randomly choosed. After a while the trajectory tend to be organized and a flock emerges.

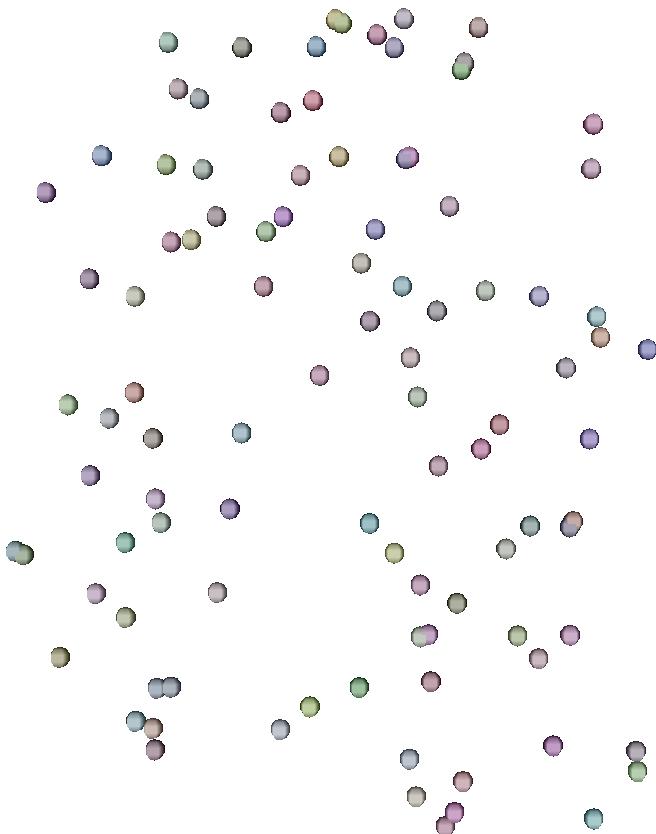
flocking birds in MGS (initial state)
flocking birds in MGS (initial state) flocking birds in MGS (initial state)
flocking birds in MGS (initial state)

flocking birds in MGS (initial state)

flocking birds in MGS (initial state)

Click on a picture to enlarge the view.


You can download a short-movie (.avi, 2.4Mb) that shows the trajectory of the birds (the last 10 positions of each bird are pictured as a coloured bead). This file can be displayed using an avi player. We routinely use the free VLC media player which can be installed both on Unix or Windows plateform.

 

 

The corresponding MGS program
specifying the 3 steering rules
record Position = {x, y, theta};;

delaunay(2) E2 =
  \e.if Position(e)
     then (e.x, e.y)
     else ?("bad element type for E2 delaunay type")
     fi
;;
 A bird is represented as a record containing its position (x,y) and the direction theta of its move. We specify a new record type Position that holds these information. The name of this type can be used as a predicate to check if a value satisfies this type.

To define a Delaunay collection type in MGS, one has to give a function that extract a position in an euclidean space from the element of the collection. Here the function that defines the Delaunay type E2 simply checks if the element has the good type and extract the position from the record fields to return a sequence of two elements (vecause the Delaunay is done in a plane).
nb_birds := 50 ;;        // number of birds
speed    := 0.5 ;;       // nominal speed
speed2   := 1.4*speed ;; // speed when a bird try to join a bird to far
d_sep    := 1.0 ;;       // to close distance
d_bound  := 5.0 ;;       // to far distance

diametre := 0.3 ;;       // a bird is pictured as a sphere of this diameter

bruit    := 10.0 * diametre / nb_birds;;
                                            
outfile := "tmp.birds.imo";; // name of the output file for the imoview viewer

 Some constant parameter of the simulation are defined.

When a bird follow the alignment rule, a noise is added to the computed direction. This noise is smaller as the number of birds increase.
fun distance(a, b) =
    let dx = a.x - b.x
    and dy = a.y - b.y
    in sqrt(dx*dx + dy*dy)
;;

 computes the distance between two points in R2 represented as records with two fields x and y.
fun nb_neighbors(a, acc) = acc+1;;

fun add_theta(a, acc) = acc + a.theta;;

fun to_close (orig, a, acc) = acc | (distance(orig, a) < d_sep);;

fun to_far   (orig, a, acc) = acc & (distance(orig, a) > d_bound);;

fun closer_bird(orig, a, acc) =
    let dist1 = distance(orig, a)
    in if dist1 < acc.dist then a+{dist = dist1} else acc fi
;;

fun farther_bird(orig, a, acc) =
    let dist1 = distance(orig, a)
    in if dist1 > acc.dist then a+{dist = dist1} else acc fi
;;
 The following functions are used as argument to the neighborsfold functions in the rules below. The details below are standard in the functionnal programming approach.
Detailed comments on neighborsfold and the use of the previous functions:

The neighborsfold function is a kind of fold that iterates on the neighbors of an element. It takes as argument a function f used to collect and combine informations from the neighbors. The function f takes 2 arguments: the visited neighbor and an accummulator which is corresponds to the result of the previous visit. For example if the neighbors of an element x0 are the elements x1, x2 and x3, then the expression
neighborfold(f,a,x0)
will be: f(x1, f(x2,f(x3,a))). The value a is the initial value of the accumulator argument (and the value of the call if there is no neighbor).

The operator neighborsfold is not really a function but rather a kind of macro called a special form. This is because it accepts as its first argument not any value but only a pattern-variable that appears in the left hand side of a rule. As a consequence, neighborsfold can appear only in the guards of a left hand side or in the right hand side of the rules in a transformation.

So, the function nb_neighbors computes the number of neighbors by simply adding one to the accumulator for each neighbor visited (the initial value is taken as zero). The function add_theta computes the sum of the direction theta over the neighbors.

The other functions have an additional argument. This argument is provided by partial application before using the functions as the argument of neighborsfold. As a matter of fact, every function in MGS are implicitly curryed (that is, a function with multiple arguments is expressed using a function whose result is another function). The first argument, named orig, represents the visited element. See below the calls to the function neighborsfold in the rules.

The function to_close will be used to compute if a birds is to close from one of its neighbors. The function to_far will be used to compute if a bird is to far one of its neighbors.   The functions closer_bird and farther_bird return the closer and farther bird respectively. The returned record has an additional field, called dist which represents the distance to the visited bird.

trans Flocking = {

  separation =
    a / neighborsfold(to_close(a), false, a)
    => begin
          let b = neighborsfold(closer_bird(a), {dist = 2*d_sep}, a) in
          let dir = if (random(2) == 0)
                    then b.theta + 'PI_2
                    else b.theta - 'PI_2 fi
          in a + {x = a.x + speed*cos(dir),
                  y = a.y + speed*sin(dir),
                  theta = dir}
       end;
      
   

  cohesion =
    a / neighborsfold(to_far(a), true, a)
    => begin
          let b = neighborsfold(farther_bird(a), {dist = 0}, a) in
          let dir = atan2(b.y - a.y, b.x - a.x)
          in a + {x = a.x + speed2*cos(dir),
                  y = a.y + speed2*sin(dir),
                  theta = dir}
           end;


  alignment =
    a => begin
            let phi = neighborsfold(add_theta, 0, a)
            and nb = neighborsfold(nb_neighbors, 0, a) in
            let dir = phi / nb
            in a + {x = a.x + speed*cos(dir) + random(bruit),
                    y = a.y + speed*sin(dir) + random(bruit),
                    theta = dir}
         end;
};;
 The transformation Flocking is used to make one evolution step of a E2 collection.

Rule separation applies when the bird a is to close from one of its neighbors. The closer bird is selected usinga neighborfold with an initial value beeing a record with a field dist two times the bounding distance d_sep. The function closer_bird select and return the neigbor which has the minimal distance with a (we know that this distance is less than the bounding distance).

When this rule applies, one of the two directions orthogonals to the current direction of the closest bird is chosen. This direction becomes the current direction of a.

Rule cohesion applies when a neighbor is to far. Then the current direction of a is updated to move toward the farthest neighbor and the current move is done at an higher speed.

When the previous rules do not apply, the default rule consists in updating the current a's direction to the mean of the neighbors directions. A little random noise is added to make the trajectory less regular.

In these rules, an expression like a + {x=..., y=..., ...} represents the parallel updates of a record a with the new field values x, y, etc.Fields in a that does not appear in the right argument of + are leaved untouched. The + operator denotes the asymetric merge of records.
fun genere_bird(dummy) =
    { x = random(1.8*sqrt(nb_birds)), y = random(2.3*sqrt(nb_birds)),
      theta = random(2*'PI),
      colR = random(1.0), colG = random(1.0), colB = random(1.0)
    }
;;

pre_init := map(genere_bird, iota(nb_birds, seq:()));;

init := delaunayfy(E2:(), pre_init)
;;
 The function generate_bird compute a bird at a random position and folowing a random direction. We also add 3 extra fields to assign a random RGB color to each generated bird.

An initial sequence of birds is generated by applying the previous function to a list of nb_birds elements (generated by the function iota).

This sequence is turned into a Delaunay collection E2 using the delaunayfy primitive.

graphical representation of the flockings birds
fun show_bird(b) =
    "Translated { Translation <"
    + b.x + ", " + b.y
    + ", 0> Geometry Sphere { Radius "
    + diametre + " Slices 5 Stacks 5 "
    + "Color <" + b.colR + ", "+ b.colG + ", " + b.colB + "> } }"
;;
 The following functions are used to writte in a file a 3D graphical description of the picture above. The 3D description language is described here.

The function show_bird generates the TEOMdescription of a bird: a sphere at some position and with some color.
fun show(f, c) = print_coll(f, c, show_bird,
                            "Group { GeometryList [\n\t",
                            ",\n\t",
                            "\n] }\n\nCommand Pause\n\n")
;;
 The function print_coll is a kind of map used to generates the description of the flocking by collection the description of each birds. See here a description of the predefined MGS function print_coll.
fun evol(c) = (show(outfile, c); Flocking(c))
;;
 An evolution step consist in outputing the graphical description of the flock and making one evolution step of the system.
evol[100](init);;
 Evolution steps are iterated 100 times.
system("imoview "+outfile);;
 At the end, the graphical viewer is lanched as an external process with the output file as an argument.


Back to top
 MGS examples index
 MGS home page


(currently under construction logo)
this site is under construction.
Pages started: May 2002. Last revision: 24 jully 2003.

Creative Commons License
Pictures, graphics and animations are licensed under a Creative Commons License.

English keywords for indexation: computer science, programming language, topological collections, transformation, declarative programming language, functional languages, simulation of biological processes, cell model, biological pathway, interaction network, gene regulation, signal transduction, morphogenesis, developmental biology, integrative simulation, biological organization, dynamical systems, dynamical structure, Gamma, CHAM, P system, L system, Paun, Lindenmayer, cellular automata, membrane computing, aqueous computing, artificial chemistry, GBF, Cayley graph, data fields, nested collections, rewriting, rule based programming, pattern-matching, intentional programming, compilation, interpretation, type, type inference, nested type, polytypism, catamorphism, static analysis, sequence, multiset, combinatorial algebraic topology, chain complex, chain group.