Switch of the phage lambda using Gillespie's SSA



Principles

Stochastic simulation is of interest when the number of molecules and/or the time-step between each event of the modelized system is small. The lambda phage is a virus that infects the cells of the Escherichia coli bacteria. Once having infected the bacteria, the virus has two possible developmental pathways. It can either (1) replicate and lyse (dissolve) the host cell and release about 100 progeny or (2) integrate its DNA into the bacterial DNA and form a lysogen. We describe the modelization and simulation in MGS of this phenomenon using a stochastic rule application strategy following Gillespie's Stochastic Simulation Algorithm. A complete biological description of the problem can be found here for example.

Biological Context

In the lysogenic phase, at each bacteria division cycle, the virus replicates itself silently. Moreover, in this phase, the bacteria acquires an immunity from subsequent phage infections. Under certain conditions (exposure to U.V. light for example) a lysogen might be induced: the viral DNA gets out of the bacterial DNA and undergoes a regular replication and lysys.

In short, the virus that infects the bacteria has two possible outcomes: lyse or lysogeny. According to the local environment, one of the two outcomes is chosen, the decision being under control of a small region of the genome, two genes (CI and CRO) and two promotors. This regulation region is called the genetic switch. Each of thow two proteins CI and CRO will repress the synthesis of the other one and increase its own production. Following local conditions, one of the two protein will take advantage over the other and the system will enter in either the lyse or lysogeny phase.

Regulation network
Figure 1: description (taken from [Mes05]) of the regulation network of the CI gene of the lambda phage. The RNA-polymerase is in red, a DNA strand appears in yellow and the repressor monomers that combines into dimers are in blue.

Figure 1 represents a fragment (limited to the only description of CI) of the regulation network of the transcription of the lambda phage. The protein (stated in blue on the figure) is a repressor and takes place in the transcription process of CI, by activating or inhibiting the proces. This molecule (equation (1)) is able to dimerize and monomerize. Equation (8) states the degradation of the repressor. Equations (2)-(5) describe the bond of the repressor molecules on the DNA strand. When dimers are missing (or  when only one or two molecules are present) on the DNA strand, the transcription of a molecule of CI is possible (equations (6) and (7)) while it becomes impossible when a third ones appears (equation (4)).

The translation of the network in chemical equations (the Ki correspond to kinetic constants) is:

\begin{equationarray}[c]{lcl}

Results of the Simulation

Below is given the result of seven simulations, after 2000 simulations steps, of the model (click on each picture to enlarge the view), with an initial state made of (#3 `CI, `D0, #10 `P):

Phage Lambda Phage Lambda The pictures show the system in a state where it has still not evolved into a lysogen or a lytic state.
Phage Lambda Phage Lambda The pictures show several evolutions of the system in a lysogen state.
Phage Lambda Phage Lambda Phage Lambda The pictures show several evolutions of the system is in a lytic state.

The corresponding MGS program


The translation into an MGS program is straightforward. Each equation is translated into a rewrite rule and the value of the constant C is determined by biological experiments(see [ KN05]). We give here the MGS program that describe the laws for the behaviour of Cro and CI :


trans A = {
//
// Description of Cro
//
 `Cro         ={ C = 0.005   }=> <undef>;
 #2 `Cro      ={ C = 0.01    }=> `Cro2;
 `Cro2        ={ C = 0.25    }=> #2 `Cro;
`D0, `P       ={ C = 0.05    }=> `D0, `P, `Cro;
`D0, `Cro2    ={ C = 9.768   }=> `D'3;
`D0, `Cro2    ={ C = 9.768   }=> `D'2;
`D'3          ={ C = 29.77   }=> `D0, `Cro2;
`D'3, `P      ={ C = 0.05    }=> `D'3, `P, `Cro;
`D'3, `Cro2   ={ C = 9.768   }=> `D'3D'2;
`D'2          ={ C = 245.371 }=> `D'3, `Cro2;
`D'2, `P      ={ C = 0.05    }=> `D'2, `P, `Cro;
`D'3D'2, `P   ={ C = 0.05    }=> `D'3D'2, `P, `Cro;
`D'2, `Cro2   ={ C = 9.768   }=> `D'1;
`D'1          ={ C = 245.371 }=> `D'2, `Cro2;
//
// Description of CI
//
`CI                 ={ C = 0.0025  }=> <undef>;
#2 `CI              ={ C = 0.01    }=> `CI2;
`CI2                ={ C = 0.25    }=> #2 `CI;
`D0, `P             ={ C = 0.005   }=> `D0, `P, `CI;
`D0, `CI2           ={ C = 9.768   }=> `D1;
`D0, `CI2           ={ C = 9.768   }=> `D2;
`D1                 ={ C = 15.557  }=> `D0, `CI2;
`D1, `P             ={ C = 0.005   }=> `D1, `P, `CI;
`D1, `CI2           ={ C = 9.768   }=> `D1D2;
`D1D2               ={ C = 15.557  }=> `D1, `CI2;
`D1D2, `P           ={ C = 0.086   }=> `D2, `P, `CI;
`D2                 ={ C = 399.225 }=> `D1, `CI2;
`D2, `P             ={ C = 0.086   }=> `D2, `P, `CI;
`D2, `CI2           ={ C = 9.768   }=> `D3;
`D3                 ={ C = 2022.38 }=> `D2, `CI2
};;
 The quations stated above are directly translated into MGS rewrite rules.  The reaction constants are given as arguments to each rule specification in the form of a C = statement.
fun inter(fic, coll) = (
            let somme = count(`D0, coll) +
                        count(`D1, coll) +
                        count(`D2, coll) +
                        count(`D3, coll) in
            (fic << 'iteration + "\t" +
             count(`Cro, coll)   + "\t" +
             count(`Cro2, coll)  + "\t" +
             count(`CI, coll)    + "\t" +
             count(`CI2, coll)   + "\t" +
             count(`D0, coll)    + "\t" +
             count(`D1, coll)    + "\t" +
             count(`D2, coll)    + "\t" +
             count(`D3, coll)    + "\t" +
             count(`D4, coll)    + "\t" +
             count(`D'1, coll)   + "\t" +
             count(`D'2, coll)   + "\t" +
             somme + "\t" +
             count(`D'3, coll)   + "\n"); coll);;
 Each value that wants to be plotted later has to be sent to a file (first argument of the function). The current iteration, together with all the variables of the simulation are  written to the file.
This function will be called after each transformation application onto the collection.
cpt := 0;;

fun once() =
 A['fixpoint=(\x1,x2.('iteration >= 2000.0)),
   'strategy = `gillespie,
   'interlude = inter("/tmp/sortie.dat")](bagify(((#3 `CI), `D0, #10 `P)));;
 cpt is a counter to memorize the current simulation count. After each simulation, the current counter is printed and the result of the simulation is plotted using gnuplot.
The once function excutes a simulation (that stops after 2000 reactions, that is the argument of the `fixpoint option) and calls afterwards the inter function defined above.
The strategy is specified using the `gillespie keyword of the 'strategy option.
The initial state is a multisets made of 3 occurences of `CI, one `D0 and 10 occurences of `P.
fun un_tour(x, y) =
 (system("rm -f /tmp/sortie.dat");
  once();
  close("/tmp/sortie.dat");
  "/usr/bin/gnuplot" << "set output\n";
  "/usr/bin/gnuplot" << "set term x11\n";
  "/usr/bin/gnuplot" << "set xlabel \"Time\"\n";
  "/usr/bin/gnuplot" << "set ylabel \"Population size\"\n";
  "/usr/bin/gnuplot" << "set logsc y\n";
  "/usr/bin/gnuplot" << "plot \"/tmp/sortie.dat\" using 1:3 title 'Cro2'with lines 2," +
                        "\"/tmp/sortie.dat\" using 1:2 title 'Cro'with lines 3," +
                        "\"/tmp/sortie.dat\" using 1:4 title 'CI'with lines 4," +
                        "\"/tmp/sortie.dat\" using 1:4 title 'DNA'with lines 4," +
                        "\"/tmp/sortie.dat\" using 1:5 title 'CI2'with lines 6\n";
  "/usr/bin/gnuplot" << "replot\n";
  sleep(1);
  cpt := cpt + 1;
  stdout << "Graph number " << cpt << "\n";
  "/usr/bin/gnuplot" << "set output \"phage-" << cpt << ".eps\"\n";
  "/usr/bin/gnuplot" << "set term postscript color solid\n";
  "/usr/bin/gnuplot" << "replot\n";
  sleep(1));;
 Function un_tour sends to gnuplot some instructions to plot the result of the current simulation and prints out the number of the plot. The counter is then incremented and a Postscript file is produced.
fold(un_tour, 0, 100);;
 Then the run of 100 experiments is launched.



References

Mes05

Denis Mestivier.
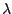Modélisation déterministe de réseaux de gènes : le répresseur $ \lambda $ du bactériophage $ \lambda $.
Notes to the spring school "Modélisation de systèmes biologiques complexes dans le contexte de la génomique" on various modelization of the $ \lambda $ phage, Montpellier, april 2005.
KN05
Céline Kuttler and Joachim Niehren.
Gene regulation in the pi calculus : simulation coperativity at the lambda switch.
Transactions on Computational Systems Biology, 2005.


Back to top
 MGS examples index
 MGS home page


(currently under construction logo)
this site is under construction.
Pages started: May 2002. Last revision: 24 jully 2003.

Creative Commons License
Pictures, graphics and animations are licensed under a Creative Commons License.

English keywords for indexation: computer science, programming language, topological collections, transformation, declarative programming language, functional languages, simulation of biological processes, cell model, biological pathway, interaction network, gene regulation, signal transduction, morphogenesis, developmental biology, integrative simulation, biological organization, dynamical systems, dynamical structure, Gamma, CHAM, P system, L system, Paun, Lindenmayer, cellular automata, membrane computing, aqueous computing, artificial chemistry, GBF, Cayley graph, data fields, nested collections, rewriting, rule based programming, pattern-matching, intentional programming, compilation, interpretation, type, type inference, nested type, polytypism, catamorphism, static analysis, sequence, multiset, combinatorial algebraic topology, chain complex, chain group.