
Although surfaces refinement operations by mesh subdivision are intuitive and easy to describe locally, their formal and global specifications in a standard language are not trivial to implement. One may wonder how cellular complexes can be used as position space of topological collections and patches (an extension of standard transformation on cellular complexes) to program such structural modifications.
In this example, patches will be used to declaratively and locally describe a subdivision algorithm and keep a good expressiveness.
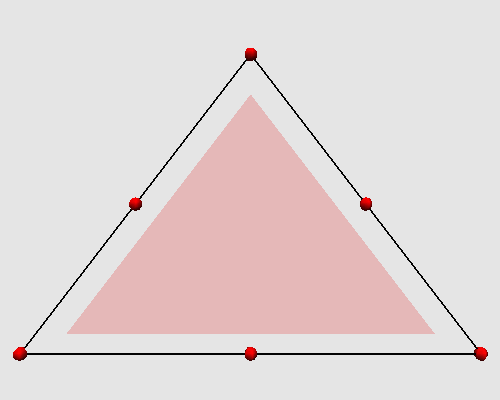
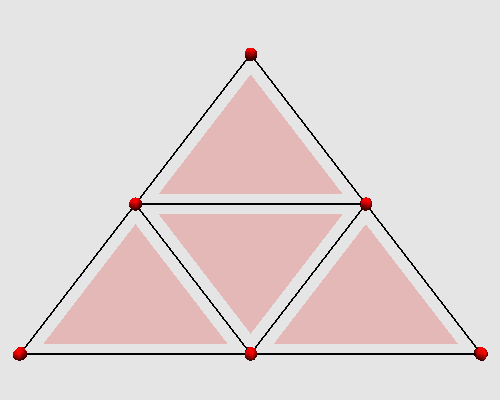
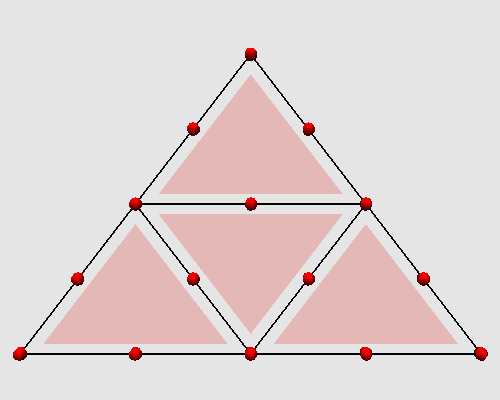
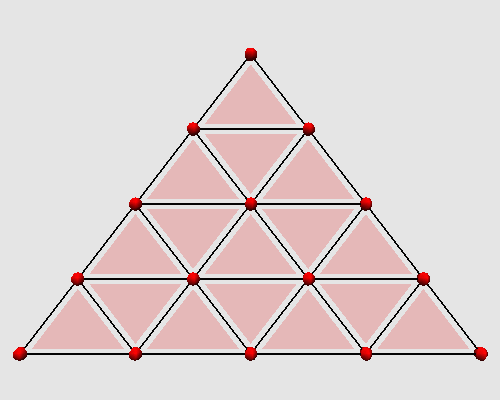
We focus here on one of the simplest algorithms of triangular meshes subdivision, the polyhedral one. It consists in dividing each triangle into four coplanar triangles.
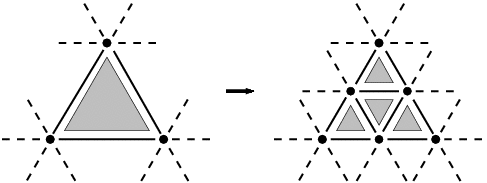
The position of added vertices is computed along the process. Here, we insert new vertices in the middle of edges (i.e. its coordinates are the average edges ones). In other algorithms, the same topological modification is used, but positions of new and old vertices are different in respect with a specific mask. This difference is only geometrical without influence on the topological structure.
The previous figure shows that although the transformation is local, some effects appear on the sides of the triangle. Indeed, the neighbor triangles are topologically modified by the insertion of vertices. This effect makes the implementation be complicated. So we can't used a unique straightforward rewriting rule.
We avoid this problem by programming two different steps: in the first one, a vertex is inserted on each edge. In a second time, each hexagons (indeed, the first transformation make triangles become hexagons by inserting three new vertices) is divided by adding 3 new edges and 4 triangles.
We respectively associate the values `edge and `face to the edges
and to the triangles. To make the difference between new and old vertices, an integer
is associated to each vertex and corresponds to its generation number (like a birth date).
A 3-dimensional embedding can also be associated:
This step consists in the selection of an edge in oder to insert a vertex on it.
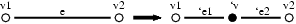
The MGS code is the following:
In this patch, v1 and v2 are not consumed (~ operator) to allow the matching of all edges that are incident to the same vertex.
Each hexagon of the mesh is substituted by 4 triangles:
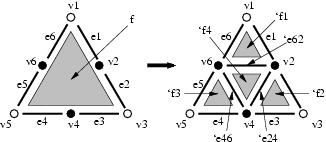
In this rule, only the hexagon f is matched
and consumed.
Its boundary is matched but not consumed to allow the building of triangles
in the right hand side of the rule.
Iterating these two steps on a triangle produces the following animation:
|
|
|
|
|
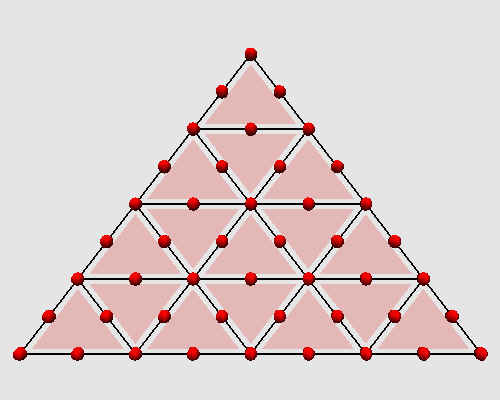
|
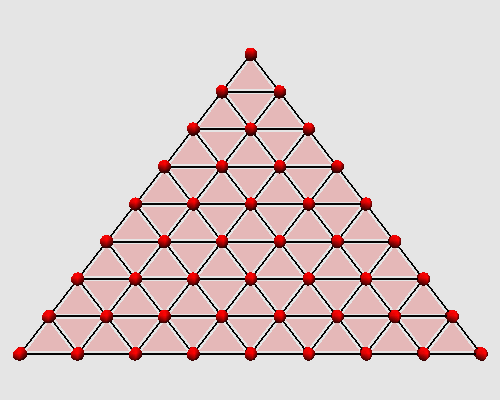
|

|

|
... |
Here are some examples of subdivisions performing by MGS.

|

|
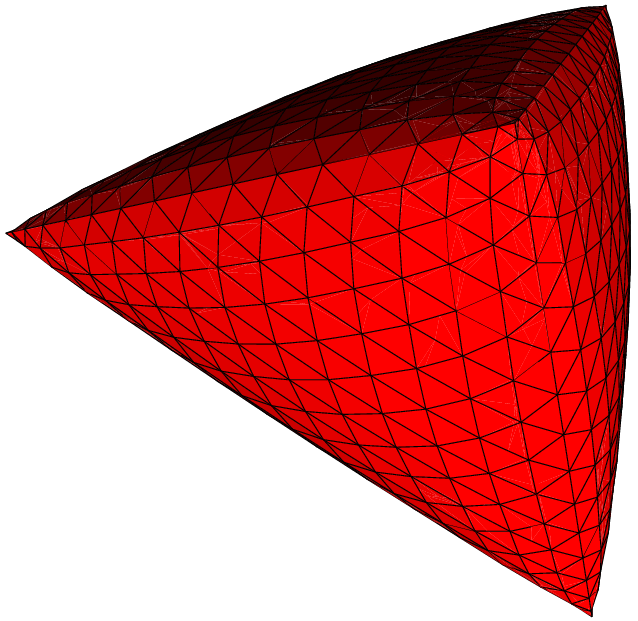
|
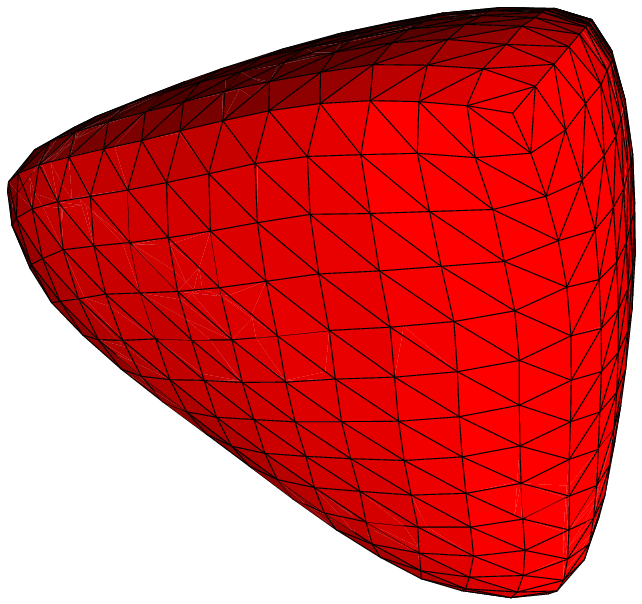
|
| Back
to top |
MGS examples index |
MGS home page |

Pictures, graphics and animations are licensed under a Creative Commons License.
|
|