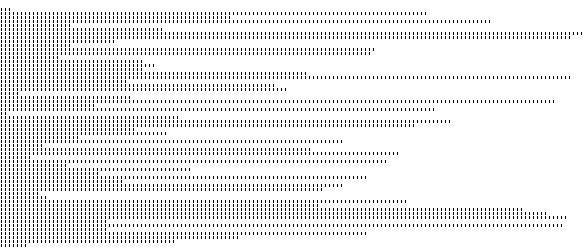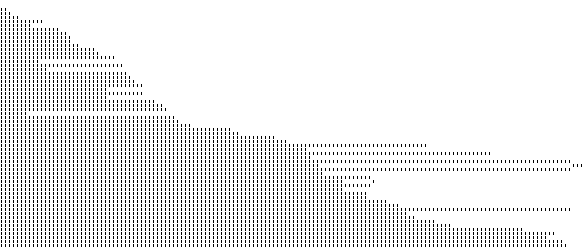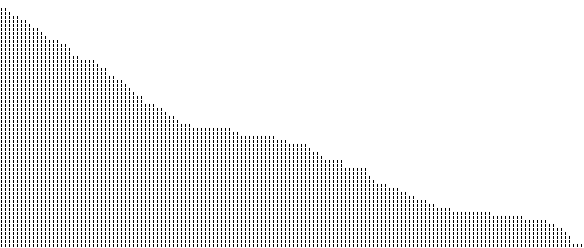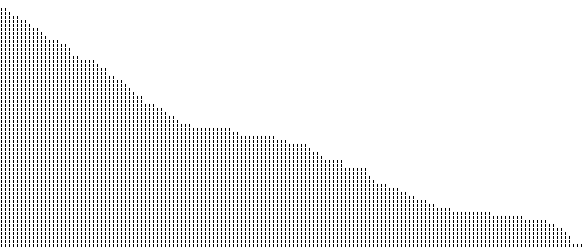
Bead sort is a new sorting algorithm designed by J. J. Arulanandham,
C. S. Calude and M. J. Dinneen (EATCS Bull. 76 (2002)). The idea is to
represent positive integers by a set of beads, like those used in an abacus.
Beads are attached to vertical rods and appear to be suspended in the air
just before sliding down (a number is read horizontally, as a row). After
their falls, the rows of numbers have been rearranged such as the smaller
numbers appears on top of greater numbers. The corresponding MGS program
is just one line long. In the following picture, a bead is rendered by a
small black ":" sign.
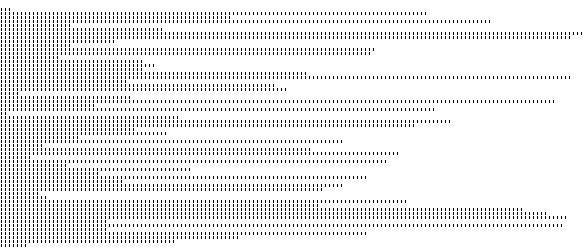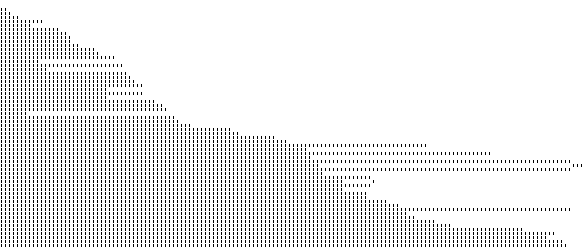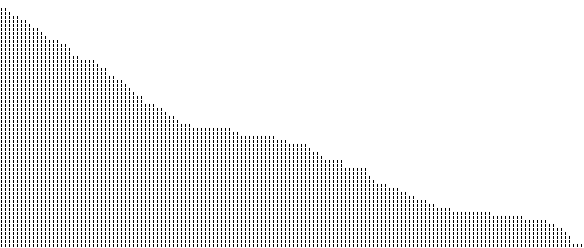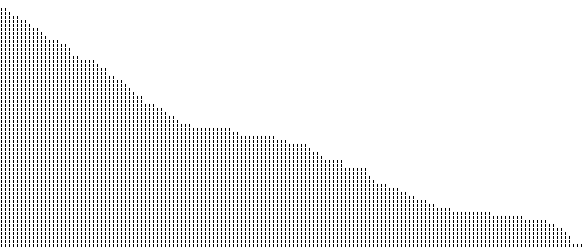
|
specifying an abacus and the bead-sort algorithm
|
|
| gbf
abacus = < rods, levels
>;; |
Definition of a GBF type.
GBF means Group Based Fields. A GBF specifies a uniform topology
where the element are indexed by a mathematical group. Here, all elements
in an instance of the GBF type abacus has two neighbors:
one following the direction rods, the other following the
direction levels. (and also two others neighbors reached following
the inverse directions). This is juste the way in MGS to define a 2D array whose dimensions are named rods and levels. |
trans do_sort = { "|" |rods> " " => " ", "|" };; |
We suppose that the numbers are
represented in unary base by a series of "|" along the levels
dimension. An "empty space" in the abacus is represented by the string "
" (this string contains only one character, the white-space). The core of bead-sorting is simply implemented as one rule that defines the exchange of a bead "|" on top of an empty space. |
| fun sort(liste)
= do_sort[*](prepare(liste)) ;; |
To sort a list of number, it is sufficient to represent
this list of number in the abacus representation and then to iterate the basic
exchange of a bead and an empty space. The optionnal argument [*]
in the application of transformation do_sort specifies
that the transformation must be iterated until a fixpoint is reached. The coding of a list of numbers into an abacus is done by the function prepare which takes a list of number as an argument. |
transforming a list of numbers into an abacus |
|
| fun
int_to_nat(x) = if (x == 0) then seq:() else "|",int_to_nat(x-1) fi;; |
Take an int x and return
a sequence of "|". The length of this sequence is x.
This function uses a simple recursion on x. Example : int_to_nat(3) returns "|", "|", "|" |
| fun
produce_zeros(n) = if (n == 0) then seq:() else " ",produce_zeros(n-1) fi;; |
Produce a sequence of n elements "
". Example : produce_zeros(4) returns " ", " ", " ", " " |
| fun
pad(len, v) = v,produce_zeros(len-size(v));; |
Takes an integer len
and a sequence v and completes the sequence v by leading
" " to build a final sequence of length len. Example: pad(5, ("|","|","|")) returns "|", "|", "|", " ", " " |
| fun max_of_list(l)
= if (l == seq:()) then 0 else max(hd(l), max_of_list(tl(l))) fi;; |
Computes the maximum of a list of integers by recursion
(hd and tl gives the head and the tail of a sequence, seq:()
denotes the empty sequence). Note that others methods are possible, e.g. using a fold operator : fold(max, 0, s) returns the maximum of the positive elements in the sequence s. |
| fun
prepare(liste) = let long = max_of_list(liste) in map((\x. pad(long)(int_to_nat(x))), liste) following |rods>, |levels>;; |
Takes a list of integers and returns
an abacus. The variable long represents the maximal number in the list, and hence, the width of the abacus. Each element in the list is transformed into a sequence of "|" padded to this width. So the first argument of following (an infix operator) is a list of lists. The second argument of following is a sequence of directions in a GBF. Each level of the nested lists is mapped into the corresponding direction into the second argument. For example, (a, a, a) :: (b, b) :: (c, c, c, c) :: seq:()returns the the abacus a, a, a(we assume that the rods dimension is mapped horizontally and levels is mapped vertically). |
| Back to
top |
MGS examples index |
MGS home page |

Pictures, graphics and animations are licensed under a Creative Commons License.
|
|