Cellular complexes allow to create various kinds of neighborhood. One of the advantages of MGS is applying a transformation dedicated to a homogeneous topological collection (as GBF collections are, where each element has a constant number of neighbors), on a topological collection whose neighborhood is heterogeneous.

As an example, in this page we will see the application of transformations that correspond to cellular automata, on 3D geometrical meshes.

Diffusion Limited Aggregation

This automaton is standard: it model some that diffuse in a medium. Some of them are fixed while others can randomly move. The behavior of praticules is given by two very simple rules:

1. Aggregation: if a mobile cell meets (= is a neighbor of) a fixed particule they glue to each other and the mobile cell becomes fixed:
2. Diffusion: if a mobile particule is in the neighborhood of an empty place, it moves for the free one, and leaves its own place empty.

the program of this transformation is as following:

We can note this transformation doesn't depend on the topological collection it is applied on.

If the transformation DLA is applied on a hexagonal grid, we obtain the following result:

Click on a picture to enlarge the view.
DLA on a regular structure: a hexagonal grid.

We will apply DLA on a sphere where the facets are considered as particule potisions. We have also choosen that two particules are neighbors if they are on two facets that share an edge. One can note this neighborhood corresponds to a Von Neumann neighborhood on a square grid. On the opposite, if we consider they are neighbors if the facets share a vertex, the Moore neighborhood is used. The neighbhood is not constant on a sphere. Indeed, on the mesh we use, poles are built with triangles (each facet has 3 neighbors) while the others are squares (4 neighbors). The following figures show the state of the sphere at t=0, after some iterations, and when a fix point is reached:

One can apply this transformation on various kinds of objects: as examples, a Klein bottle that is not orientable, or a chess pawn that is topologically equivalent to a disk.

Ants foraging for food...

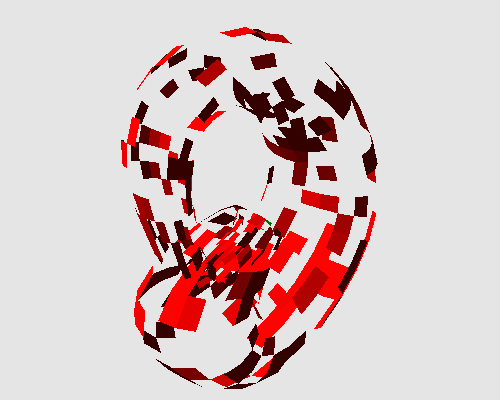
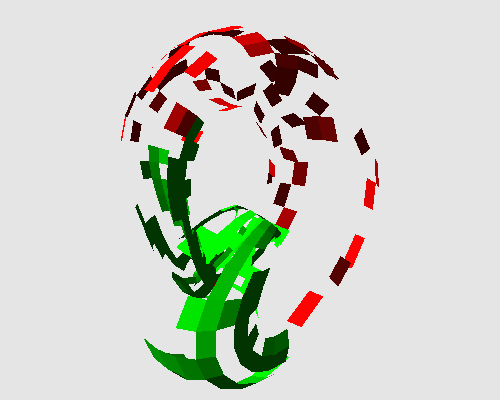
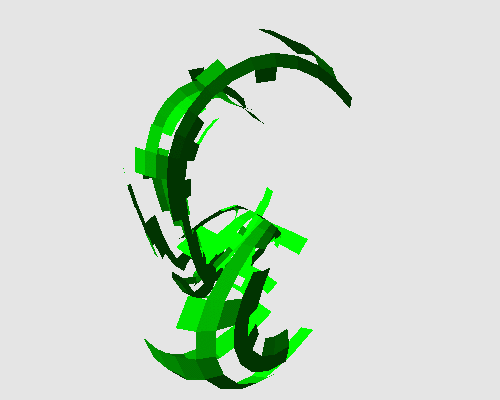
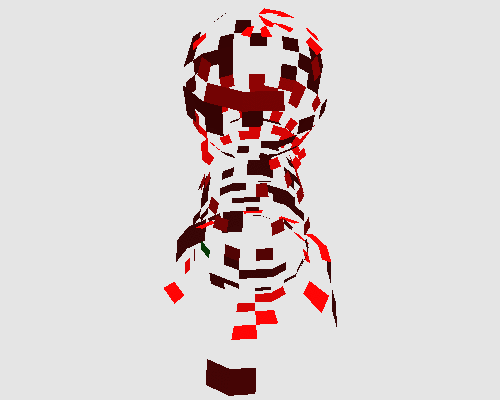
In this second example, we use the model of ants that forage for food behavior described here. Like the DLA, this transformation is applied without any modification, on a spehere. An animation can be available here (4.3 Mo). The black cells are ants that are searching for food, the yellow ones are coming back to the niddle. The niddle is blue and the food is green. The transparent red traces correspond to a chemical left by the ants while they are coming back home. It is used to keep in mind a path from the food site to the niddle. The transparency degree means the substance is evaporating.

this site is under construction.
Pages started: May 2002. Last revision: 24 jully 2003.

Pictures, graphics and animations are licensed under a Creative Commons License.