
During pluricellular organism growth, two characteristics are interesting to be
highlighted:
In this example, we will see haw MGS can be used to model phenomena such as neurulation.
The neurulation process consists in a topological modification of the back region of the embryo (cf figure above): the neural plate is folding and forms the neural fold. Then, this folding curves the neural plate until the two borders touch each other and make the plate become a neural tube. A last step consists in a separation between the neural tube and the epidermis located at the neural crest. The topological modification corresponds to the transformation of a plate into a tube and is not trivial to implement.
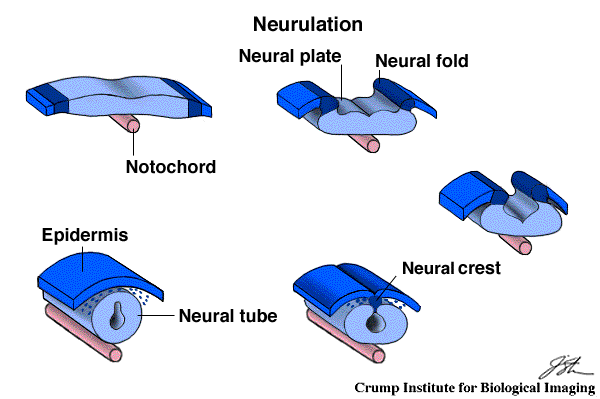 Diagrammatic description of the neurulation process taken from a drawing by Patricia Phelps |
 Neural Fold Closure Through cell shape changes, the neural plate curls forming a neural fold on each side. The neural folds come together and fuse along the dorsal midline producing the closed Neural Tube. animation taken from Bill Wasserman's Developmental Biology Page |
In our example, we have simplified the systems into a sheet of epithelial cells that is folded by local cell migration and deformation. After the migration, cells that were on the opposite sides at the beginning become very close to each other. Once they are closed enough, they glue together to make the original sheet of cells become a cylinder.
The mechanical model we use is inspired from works described in [Odell et al., 1981] and in [Nagpal, 2001]. An epithelial cell is a cube composed by a volume where the genetic code can be stored, 6 faces considered as exchange interfaces between cells, 24 edges (12 are the classical boundary of the 6 faces, and 12 are diagonals of the faces) also called fiber, that simulate the cytoskeleton, and 8 vertices.
In this example, we will only use cells of dimension 0 and 1. In fact, Odell associates a spring in parallel with a friction element to each fiber. By modifying the rest length and/or the stiffness constant of springs, the cell can be deformed.
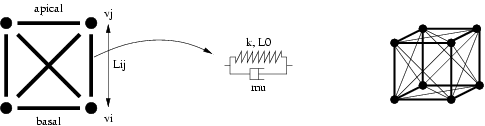
we will define a type to the values associated to each cell:
record Vertex = {Type Vertex is a record composed by 10 fields used within the newtonian mechanical: px, py and pz represent the position vector, vx, vy and vz the velocity vector, ax, ay and az the acceleration vector, and m the mass.
record Edge = {The type Edge pulls together the different constants associated to the spring model k, mu and L0. The velocity of the elongation is stored in the field vL. Moreover, two fields, vi and vj refer to boundaries of the edge; they are used to generate an arbitrary orientation of the edges.
At the initial state, on considers a nxm epithelial cells matrix.
System structure deformations are simulated by a mechanical model. Here, we compute the vertices movements caused by springs forces. This is done by two transformations:
trans <1> update_spring = {This transformation acts on the 1-dimensional elements of the collection it is applied on (denoted by trans <1>). It computes for each edge e the elongation speed of the spring stored in e.vL. The force applied on the extremities of e is also computed as a vector.
trans <0> integration [delta_t = 0.01] = {This second transformation deals with the vertices. For each vertex vi , vi incident edges forces are summed. We can note, the orientation of edges is considered in this sum. We use Newton's second law of motion to compute the acceleration of the vertex. Then, acceleration is integrated twice by a classical Euler approximation to obtain the velocity and position vectors. Time step is given by delta_t, an option of the transformation.
A movie, available here (8.4M), shows the effects of a these transformations on a 20x2 matrix of cells.
In the previous movie, the end is not the one expected. Indeed, collisions of boundaries have to be checked, and boundaries have to be "sewed" to form the cylinder. This operation can be represented as follows:
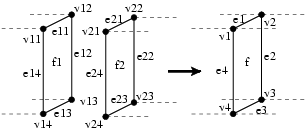
Then, the transformation can be written:
patch surgery = {The pattern sums up the previous figure. The predicate P checks that faces f1 and f2 are closed enough to be merged. In the right hand side, a new face that corresponds to the f1 and f2 merging, is built. Function average_i(a,b) compute the average between the values associated to the both i-cells a and b. Function unmatched_cofaces returns the list of common cofaces of its arguments, except already matched elements.
The following screen shots present the topological surgery:
 |
 |
 |
A movie is available here (6.6M).
To be sure the cylinder is really closed after th surgery step, we will insert in 3-dimensional cells a token that will diffuse. When it is at a boundary, it can obviously not leave the sheet. After the topological modification, there are no boundaries anymore and the token can diffuse. We suppose that there is only one raw of cells ; the system becomes a filament of cells that is folding until it forms a ring. The transformation is as follows:
trans <3,2> token = {At the initial state, all volumes have the same value `cell, except for two contiguous one respectively marked by `token (it is the one which contains the token) and `back. The `back mark imposes a direction to the token. Indeed, the first rule shows the token can only diffuse to an empty cell, and it is followed by the token `back. In the second rule, the token can't go forward, and swap its place with the token `back, to go in the opposite direction.
A movie is available here (3.6M).
[Odell et al., 1981] Odell, G.-M., Oster, G., Alberch, P., and Burnside, B. (1981). The mechanical basis of morphogenesis. i. epithelial folding and invagination. Developmental Biology, 85(2):446 462.
[Nagpal, 2001] Nagpal, R. (2001). Programmable Self-Assembly: Constructing Global Shape using Biologically-inspired Local Interactions and Origami Mathematics. PhD thesis, Massachusetts Institute of Technology.
| Back
to top |
MGS examples index |
MGS home page |

Pictures, graphics and animations are licensed under a Creative Commons License.
|
|