
Bien que les opérations de raffinement de surface par subdivision du maillage soient intuitives et faciles à décrire localement et schématiquement, leurs spécifications formelles et globales dans un langage standard ne sont pas immédiate et facile à implanter. On peut alors se demander dans quelle mesure on peut utiliser les complexes cellulaires comme espace d'indexation de collections topologiques et les patches (extension des transformations standards sur les complexes cellulaires), pour programmer de tels changements de structure.
Dans cet exemple, nous allons voir l'utilisation des patches pour décrire déclarativement et localement un algorithme de subdivision de surface, tout en conservant une bonne expressivité.
On se concentre ici sur l'un des plus simples algorithmes de subdivision de maillage triangulaire, qui consiste à diviser chaque triangle en quatre triangles coplanaires. Il s'agit de la subdivision polyhédrale.
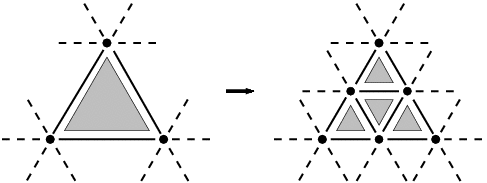
La position des nouveaux sommets est calculée au cours de la subdivision. Ici, on choisit que chaque sommet est inséré au milieu d'un arc (c'est-à-dire que ses coordonnées sont la moyenne des coordonnées des arcs du triangle. D'autres algorithmes utilisent la même modification topologique mais placent les nouveaux et les anciens sommets à des positions différentes, suivant un masque particulier. Il ne s'agit là que d'une différence géométrique qui n'a d'influence que sur le plongement du maillage topologique dans l'espace euclidien.
On peut voir sur la figure précédente, que bien que la transformation soit locale, des effets de bords apparaissent. En effet, les triangles voisins voient leur topologie changer par l'insertion des sommets. C'est cet effet de bord qui rend l'implantation de l'algorithme compliquée. On ne peut donc pas utiliser cette règle directement.
Pour éviter ce problème, nous appliquons deux modifications successives pour obtenir le résultat. Dans premier temps, on rajoute un sommet sur chaque arc. Dans une seconde étape, chaque hexagone (en effet, la première transformation a pour effet de rajouter 3 sommets par triangle produisant alors des hexagones) est divisé par l'ajout de 3 nouveaux arcs en 4 triangles.
On associe respectivement les valeurs `edge et `face aux arcs
et aux triangles.
Pour faire la différence entre les anciens sommets et les nouveaux sommets
lors de la deuxième étape, on associe un entier à chaque sommet, correspondant
à sa génération. On associe également le plongement dans l'espace :
Cette étape consiste à sélectionner chaque arc, pour y insérer un sommet.
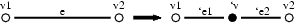
Le code MGS est la suivant :
Dans ce patch, v1 et v2 ne sont pas consommé (opérateur ~) pour autoriser le filtrage de tous les arcs incidents à un même sommet.
On cherche dans le maillage chaque hexagone pour les remplacer par 4 triangles :
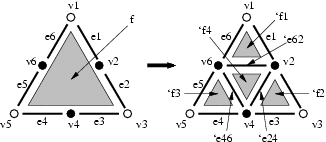
Dans cette règle, seule l'hexagone f est filtré et consommé. Son bord est filtré mais non-consommé pour permettre la construction des triangles en partie droite de la règle.
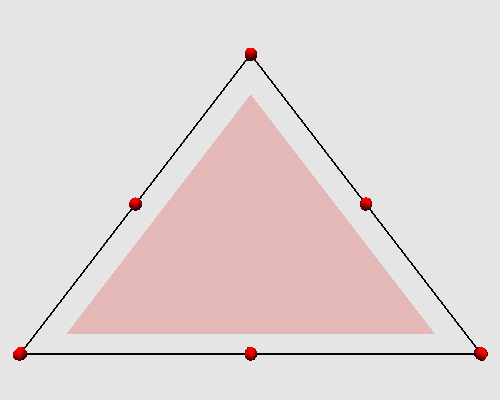
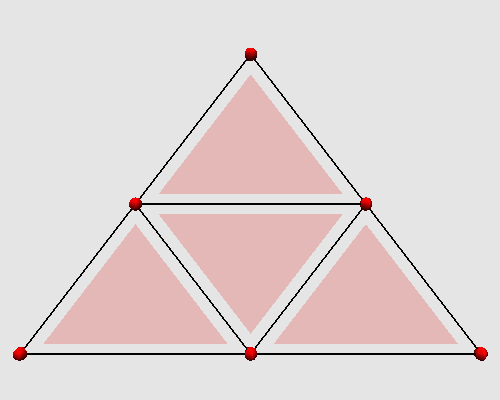
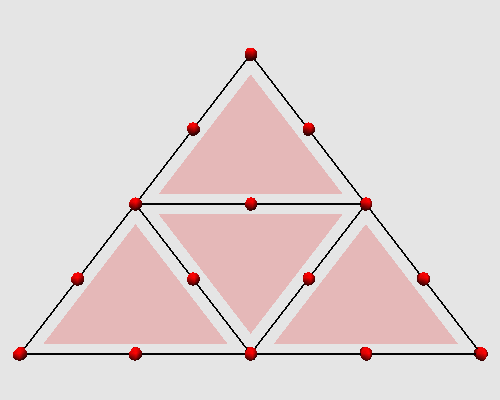
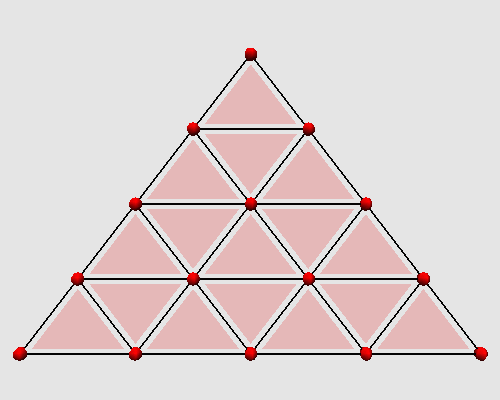
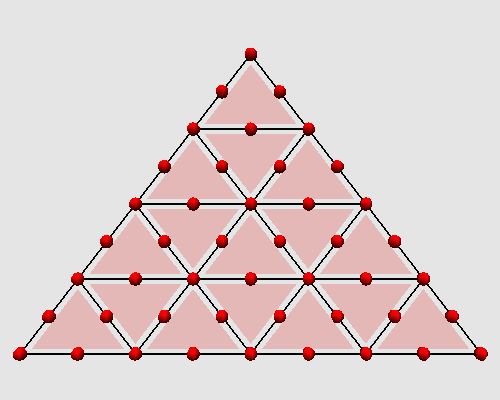
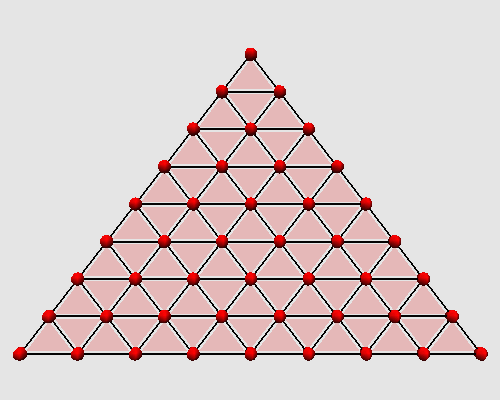
L'itération des ces deux étapes successives produit sur un triangle l'animation
topologique suivante :
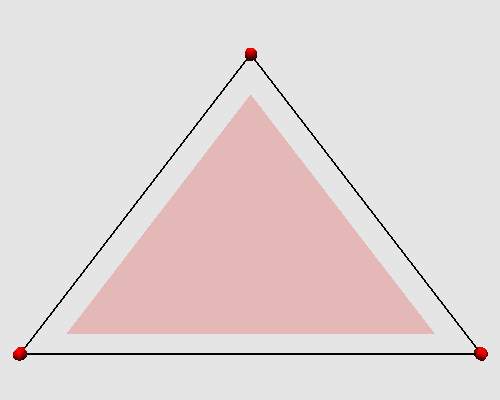
|
|
|
|
|
|
|

|

|
... |
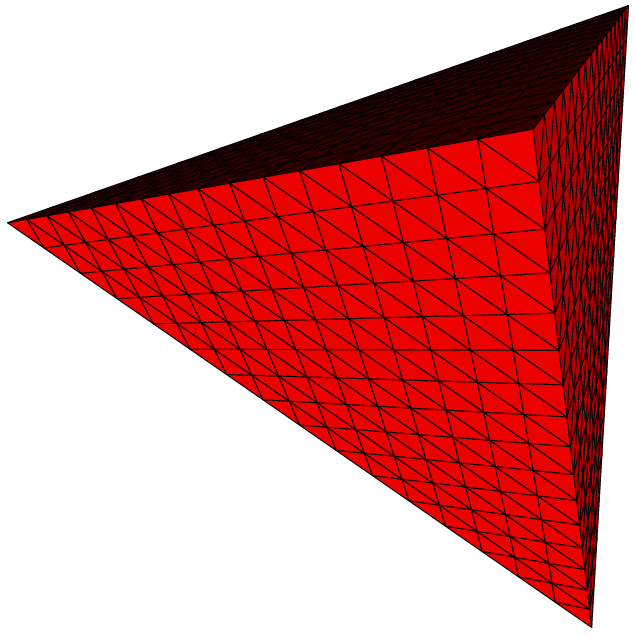
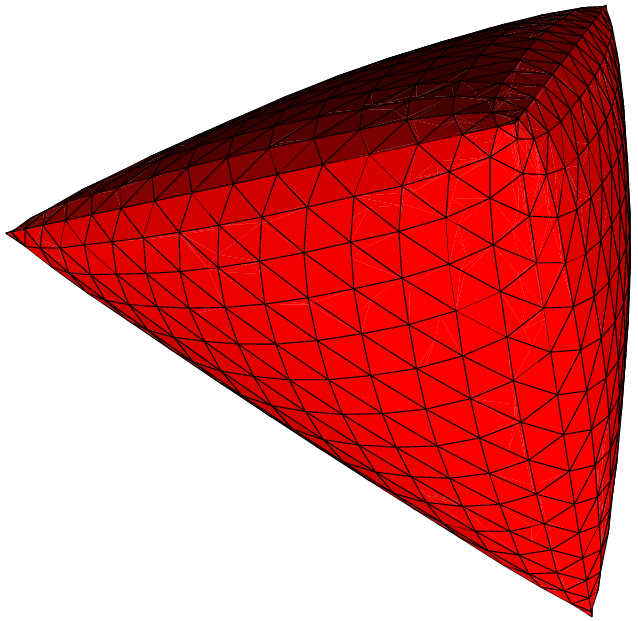
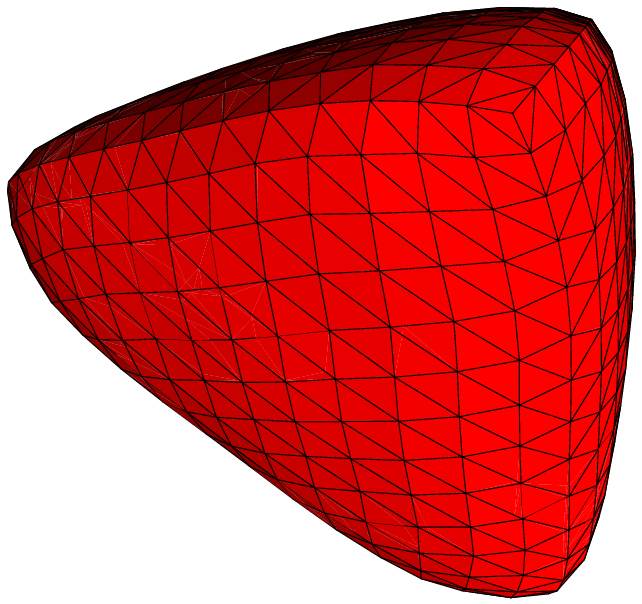
Voici quelques exemples de subdivisions réalisées en MGS.

|
|
|
|
| Back
to top |
MGS examples index |
MGS home page |

Pictures, graphics and animations are licensed under a Creative Commons License.
|
|