
Dans cet exemple, nous nous intéressons à l'implantation d'un modèle biologique complexe inspiré des travaux de Bottino et al. Ce modèle simule le déplacement du spermatozoïde du nématode Ascaris suum.
Le spermatozoïde d'Ascaris suum se déplace en suivant un cycle lamellipodial protusion, adhésion, rétraction. Les mécanismes chimiques du déplacement se situent dans la partie avant de la cellule, appelée lamellipodium. Dans ce modèle, le système se résume à la membrane du lamellipodium en contact avec le milieu extérieur (ou matrice). Dans un premier temps, une polymérisation produit un gel fibreux à l'avant de la cellule, créant alors des protusions. Celles-ci poussent la membrane en avant. Une quantité d'énergie élastique apparaît alors dans le gel. L'avancée de la membrane vers l'avant vient alors se coller à la matrice lors de la phase d'adhésion. Un processus de traction entraîne le corps de la cellule à se déplacer. Le gel fibreux subit pendant cette phase une contraction. La dernière étape est localisée près de la frontière entre le lamellipodium et le corps de la cellule : une dépolymérisation du gel entraîne la désadhésion de la membrane et libère une quantité d'énergie tirant le corps de la cellule vers l'avant. Ces mécanismes dépendent d'un gradient de pH.
Bottino décrit ce processus de déplacement à travers des équations différentielles continues correspondant aux efforts élastiques et de tensions dans la membrane fixée à la matrice extra-cellulaire, et à la distribution de pH dont les équations mécaniques dépendent. Ces équations sont ensuite traduites sous une forme discrète à l'aide d'un modèle à éléments finis. La membrane est partitionnée au moyen d'un graphe de Delaunay.
La traduction en terme de collection topologique et de transformations de ce modèle est assez immédiate.
Un noeud du graphe de Delaunay est un enregistrement composé de 8 champs :
Les champs px et py représentent la position du noeud dans l'espace, vx et vy sa vitesse, et H et pH la concentration en protons et le pH. On définit sur les éléments de type Node, des prédicats pour déterminer le type exact du noeud.
Le graphe de Delaunay est décrit par :
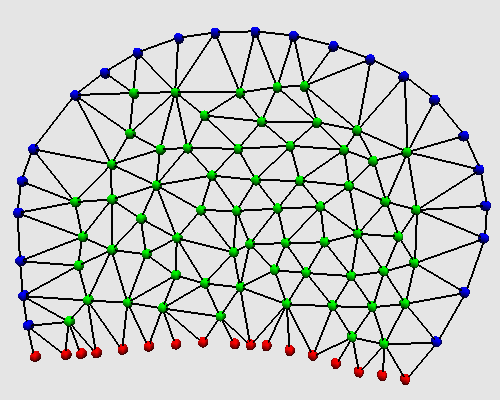
La polymérisation et la dépolymérisation sont implémentées sous la forme de règles
de réécriture ajoutant ou supprimant des noeuds :
où length retourne la longueur d'un arc entre deux noeuds.
Les équations de diffusion du pH sont traduites sous la forme d'une fonction donnant le
nouveau pH d'un noeud en fonction des noeuds voisins :
Les deux premières règles correspondent aux conditions aux bords. La dernière règles applique l'équation de diffusion pour tous les noeuds internes (Inode). On remarque l'utilisation de la primitive neighborfold pour calculer la contribution des voisins.
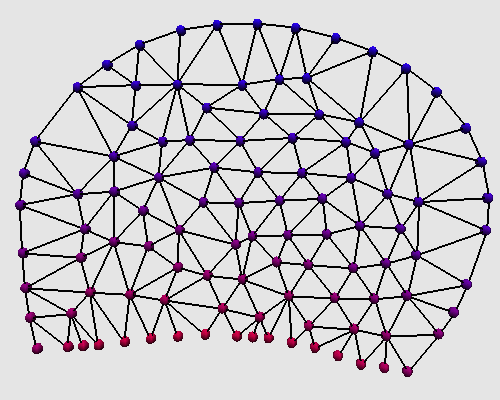
La transformation calculant les forces s'appliquant sur chaque noeud du graphe, et mettant à jour la position de ces noeuds, est équivalente à celle de la diffusion de pH. On ne la précisera donc pas ici. L'animation est téléchargeable ici (2.8 Mo).
| Back
to top |
MGS examples index |
MGS home page |

Pictures, graphics and animations are licensed under a Creative Commons License.
|
|